Что такое линейность измерительных приборов и почему она так важна ?

Дисплей измерительного прибора как он бы он ни был - сенсорный, жидкокристаллический или светодиодный - не суть важно какой, всего лишь визуальное отображение электрических сигналов на выходе микросхемы - аналогово-цифрового преобразователя (микроконтроллера, микропроцессора). На пути от датчика (старт) до дисплея (финиш) могут быть фильтры, усилители, преобразователи. Но в любом случае все манипуляции после датчика производятся уже с электричеством. Другого "языка" приборы не понимают. Более того, прибор понятия не имеет о том, что есть такой элемент, как датчик. Прибор работает только с электрическими сигналами. Ему абсолютно все равно, датчик ли выдает сигнал ему для обработки или вы вмешаетесь в схему и подмените датчик, подав таким образом один из электрических параметров вместо него.

У каждого компонента измерительного прибора своя миссия. И все эти компоненты работают как слаженный оркестр. А кто ж дирижер ? Пусть это будет человек, держащий в руках прибор. Наш предок - это человек прямоходящий (Homo erectus). Ему на смену пришел человек разумный (Homo sapiens). А у нас выходит следующая реинкарнация - "человек измеряющий" (Homo metiens - так это будет по латыни). То есть Homo metiens — это индивид, который не может жить без влагомера, pH-метра и пирометра. Шутка. Хотя для мастеров в той или иной отрасли это на 100 % верно. Без приборов они как без рук.
И им важна точность и достоверность. И сегодняшняя тема позволит приоткрыть одну из дверей "кухни" измерительных приборов.

Введение в линейную измерительную функцию

Главная миссия у датчика - воспринять физическую величину (освещение, влажность, кислотность) и перевести ее в электрический импульс.
Отметим ключевой момент для нашей сегодняшней беседы - есть входная величина, а есть выходная. Это строительный материал для функции. При одном условии - должно быть правило, закон, т.е. мы должны точно знать, при каком значении входной величины, какую мы получим выходную величину. В идеале так должно быть. На практике же есть набор возмущающих факторов, которые стремятся исказить это соответствие и внести элемент неопределенности (говоря заумным словом "энтропия").

Голубая мечта всех производителей - чтобы во всем диапазон измерения прибора функция его датчика была линейной.

Пример из области ph метров. Вот частичное задание функции в табличном виде. Это идеальный (линейный) случай. Та самая мечта. При изменении PH на 1 единицу, напряжение на выходе PH электрода меняется строго на 59,16 мВ.

Практически все ph-метры имеют диапазон 0-14 PH. Так вот, если на всем этом диапазоне эта линейная зависимость соблюдалась бы, это была бы и техническая реализация (воплощенная в металле и пластике) мечты инженеров - разработчиков того или иного бренда.
Почему ? Причин несколько.

1. Прогнозируемость и предсказуемость. Мы можем абсолютно точно знать в ЛЮБОЙ точке графика значение функции (мВ), если зададим значение PH. Это дорогого стоит. Это все равно, что человеку знать, что будет на протяжении каждого дня его долгой жизни. Только захочет ли он это знать ? Вопрос. А вот для измерительных приборов (и разработчиков вместе с ними) прогнозируемость это настоящее счастье. Если можно оперировать этим человеческим понятием в этом контексте.
2. Простота и быстрота расчета. Линейная функция требует очень малых математических мощностей для расчета. Даже в уме можно посчитать значение. Что к сожалению человечество утрачивает, полагаясь сначала на калькуляторы, а ныне на смартфоны. Поскольку имеем всего 2 элементарные математические операции - умножение и сложение. Вот формула для ph-метров: E=E0−59,16×pH. Как видим, типичная линейная функция. E0 - начальное смещение верх-вниз графика в зависимости от знака, а 59,16 - коэффициент, определяющий крутизну функции (скорость возрастания или падения). Самые энергоемкие и медленные операции, нагружающие процессор - это возведение в степень и извлечение корня, дифференцирование / интегрирование.

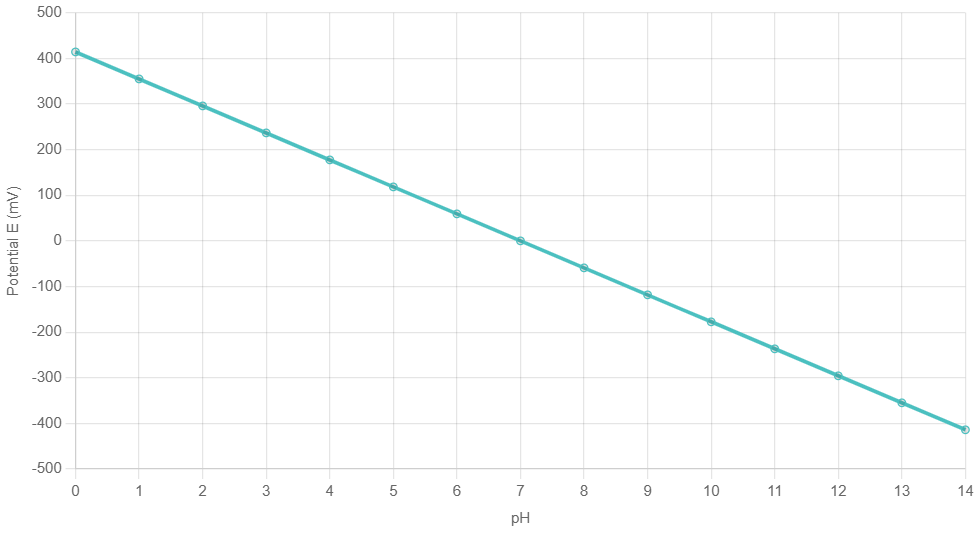
Так что прямая линия, а соответственно линейная, прогнозируемая и простая функция это красота.
А вот например для квадратичной функции (не будем приводить здесь ее график, чтобы не засорять пейзаж), то есть всем известная школьная парабола, с ростом X все резче взмывает вверх Y (значение функции).
"А что, разве парабола не предсказуемая ?" - восклинет вдумчивый и хорошо математически подкованный читатель. И будет прав. Ведь квадратичная функция тоже описывается однозначной формулой y=x², по которой можно рассчитать значение y при ЛЮБОМ x. То есть для функций, даже нелинейных, которые на всем области определения можно описать формулой (не приблизительной с допустимой степень погрешности, а точной), правило прогнозируемости и предсказуемости безусловно выполоняется. Чего кстати не скажешь о простоте и быстроте расчета. Возведение в степень, особенно с большими показателями степени, довольно трудоемкая операция для процессора.

Мир нелинейностей

Приведем пару примеров.
На самом деле мы живем в мире нелинейностей. И часто с ними можно мириться. Вот несколько примеров из разных сфер.

• Заряжание аккумулятора (зависит от модели - у Вас может быть по-другому). Можно заметить, что время на заряд 1 % емкости в диапазоне 0-90 % может быть в 1,5-2 раза меньше (то ест зарядка идет быстрее), чем на тот же 1% от 91 до 100 %. Такое впечаиление, что кто-то мешает аккумулятору и не дает ему заряжаться. Да, здесь может влиять: температура батареи, особенности злектрохимических процессов в начале и в конце цикла заряда (быстро или медленно берет заряд). И зарядное устройство может автоматически уменьшать ток ближе к концу заряда. Но причина не важна - график заряда нелинейный.
• Зависимость ошибки пирометра от температуры. Это особено заметно по высокотемпературным (широкодиапазонным инфракрасным термометрам), как например для IR-870 FLUS (одного из ТОПовых промышленных), представленным у нас на сайте. Например при -10 ℃ ошибка составит ±4℃, для 100 градусов ±2℃, для 1000 ±2℃. Это особенная разновидность нелинейности - не непрерывная, а ступенчатая. При переходе через поддиапазон ошибка меняется скачком (в сторону уменьшения или увеличения). Например в диапазонах от "до 0 ℃" до "от 0 до 500℃" ошибка уменьшается в 2 раза с ±4℃ до ±2℃.

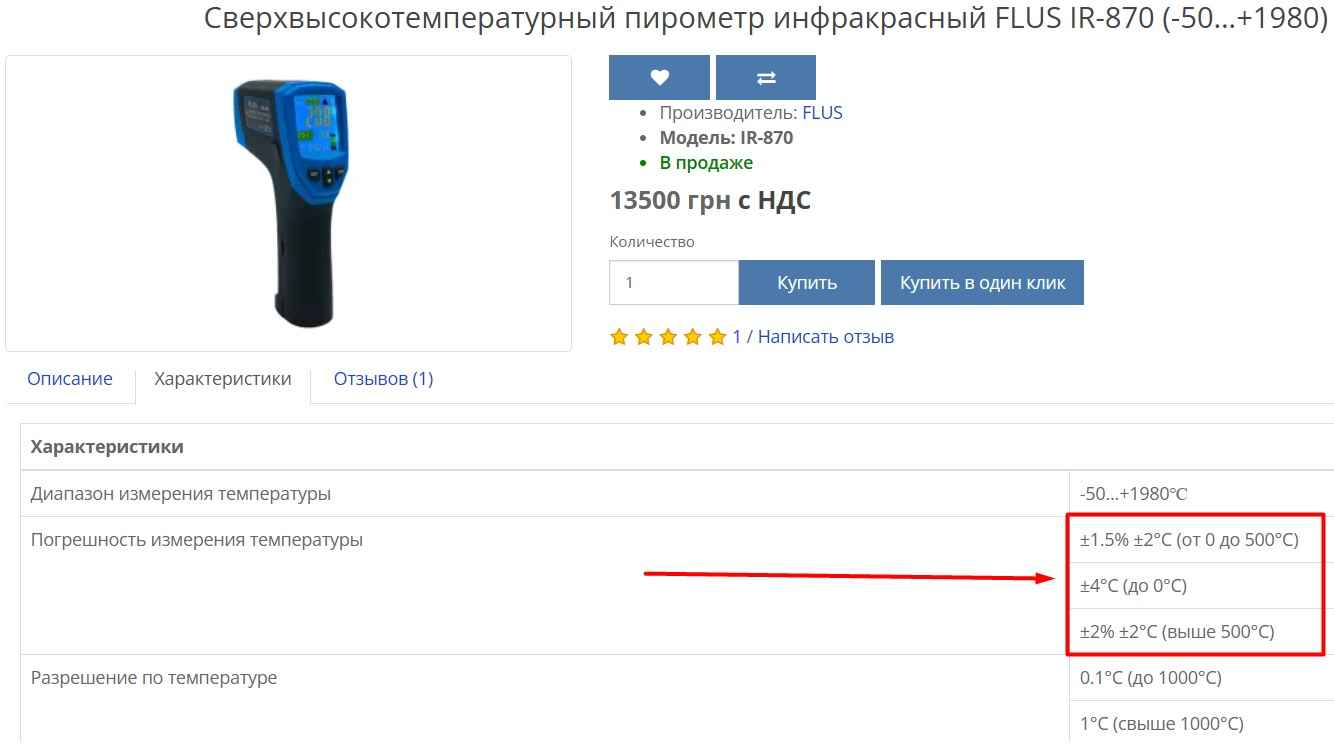
Но предсказать и прогнозировать значение нелинейной фукнции, как для параболы (или гиперболы) или вообще степенной и любой другой нелинейной функции, можно далело не всегда. Особенно, если нет формулы для ее описания.
Вот мы привели выше график линейной функции зависимости разности потенциалов на ph-электроде от значения PH. Он идеальный, а в жизни измерительных приборов бывает совсем по-другому.

Как достраивать линию ?

Из курса геометрии известно, что для построения линии требуется 2 точки. Одна - мало, три и более подойдут только, если они будут лежать на одной прямой. Для ph-метров, которые имеют функцию калибровки, могут быть предусмотрена калибровка по 1, 2, 3 и более точкам.
Калибровка по 1 точке как-то не стыкуется с геометрией. Поскольку через одну точку можно провести бесконечное множество прямых. И каждая из этих прямых будет расположена под разным углом к оси. А это в свою очередь значит, что мы не сможем прогнозировать выходное значение в зависимости от входного, на всем диапазоне, кроме точки калибровки. Но то геометрия в теории, а то практика приборов... А именно, умная электронная начинка, которая "ухватывается" всего лишь за одну точку и этого оказывается достаточно для более-менее точных измерений во всем диапазоне. Это как Шерлок Холмс мог по крайне скудным начальным данным составить полную картину преступления.
Объяснение в данном случае может быть только одно. Мы задаем точку на прямой, калибруя прибор например по буферному раствору ph=7.0. А как же прибор "узнает", под каким углом будет проходить кривая прямая ? То есть как достроить прямую влево и вправо на всем диапазоне измерения PH ?

Ответ может быть только один - в приборе "зашит" алгоритм, который опираясь на результат калибровки, выбирает одну единственную прямую, и "дорисовует" недостающие ее части влево и вправо.

В этом кстати огромное преимущество и гибкость цифровых измерительных приборов перед аналоговыми. Например стрелочными.
Между прочим и в стрелочных приборах сплошь и рядом шкалы могут быть нелинейными. То есть в одном поддиапазоне измеряемая величина растет быстро, а в другом - "еле плетется". Это видно визуально - рисочки на шкале то расположены густо одна к другой, то между ними расстояние ощутимо увеличивается. Это явный признак нелинейности.
Вот это "достраивание" или "дорисовка" (мы сознательно упростили термин, чтобы упростить понимание) имеет два устоявшееся названия, от которых так и веет научностью: интерполяция и экстраполяция. Поясним. Пусть мы откалибрвали ph-метр по двум точкам: 4.01 и 7. Процесс нахождения промежуточных точек между этими двумя точками называется ИНТЕРполяция ("интер" - внутри), для чего существует набор математических инструментов. А вот "достраивание" за пределами этого интервала (меньше 4.01 и больше 7.0) называется ЭКСРАполяцией ("экстра" - вне).
Мы слишком много времени посвятили ph-метрам и частично пирометрам, но линейность шкалы желанна практически для всех остальных приборов. Особенно теперь после вышесказанного, отрываются глаза у неискушенных пользователей, которые больше выполняли рекомендации, предппсанные в инструкции, больше механически не вдаваясь, что там стоит в том или ином прибор "под капотом".
Для человека прибор - это кнопки и дисплей. А прибор живет жизнью функций, графиков зависимостей и калибровок.

• например влагомеров зерна от торговой марки Supertech (Дания). В них можно ввести поправочный коэффициент и прибор переместит - поднимет вверх или вниз (в зависит от знака вводимой поправки + или -) калибровочную прямую, тем самым приближаясь к истине уменьшая ошибку. Для введения поправочного коэффициента требуется стандартный образец зерна - эталон и по сути это аналог буферного раствора (с заранее заданным PH).
• в некоторых шумомерах, даже недорогих (а уж в шумомерах первого класса это как говорят англоязычные - must have) есть возможность подстройки - обычной отверткой в простейшем случае по источнику эталонного звука заданной интенсивности и частоты. Это источник называется калибратор. И этот калибратор (уже по названию понятно для чего он нужен) по сути очень близкий аналог камертона, по которому настраивают музыкальные инструменты. В момент настройки (калибровки) шумомера его измерительная фукция (прямая зависимости) также движется немного вверх или вниз.
• даже такой оптический инструмент который и измерительным прибором как-то язык не поворачивается назвать - уж слишком он прост, как рефрактометр - в нем нет ни электроники (если не брать цифровые модели), но даже в нем есть винтик, который если подкрутить отверткой, тоже двинет условную прямую (график функции) ближе к точному результату. А что является эталоном для рефрактометра ? Калибровочная жидкость - дистилированая вода или масло. Кстати для рефрактометров мы немного покривили душой, когда сказали, что калибруя его, мы двигаем условную прямую. Не только условную ! Как раз при калибровке, и нужно смотреть в глазок и мы увидим как полоска должна стать ровно по центру. Вот где-то отдаленно напоминающее подобное, только где-то в недрах микросхем, и происходит при калибровке приборов.

А крутизна ?

То есть, если прибор предусматривает калибровку по эталонному образцу, эта прямая немного перемещается вверх или вниз, чтобы уменьшить погрешность.
"Простите !" Во второй раз воскликнет внимательный и дотошный читатель. "А почему вы говорите только о том, что прямая на Вашем графике перемещается вверх или вниз". Ведь в приведенной вами формуле прямой есть множитель (например в формуле для ph-метров это 59,16), который определяет крутизну, то есть скорость возрастания или снижения линейной функции. А эту крутизну нельзя никак подстроить ? Может со временем из-за старения прибора не только прямая "уезжает" вверх или вниз, но и меняется ее угол наклона ?
Абсолютно справедливое замечание. Чтобы не крутить заезженную пластинку с приборами, о которых мы уже здесь говорили неоднократно, обратимся к лабораторным нитратомерам. Для них действительно и отдельно настраивается такой показатель, как крутизна характеристики : зависимость напряжения от концентрации ионов. И здесь не всегда удается достичь линейности ! Особенно в начале и конце диапазона, где не редко, виляя хвостом, "прямая" изгибается.

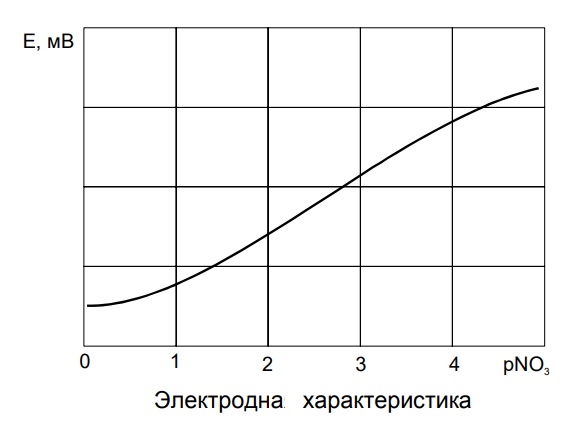
А значит никакая она уже не прямая. А нелинейная функция. "Так что получается, что для каждого участка будет своя формула ?" Да ! И теперь Вы понимаете, насколько сложнее и описывать набором формул нелинейную функцию и считать ее значение. Кстати далеко не всегда теоретически нелинейность можно описать формулой. В большинстве случаев как раз нельзя. Сделайте на листке бумаги несколько завитков карандашом и попробуйте описать эту "функцию" формулой. Нет этой формулы ! Поэтому приходится изворачиваться. Например, заменяя криволинейный участок прямолинейным. Конечно же, это приводит к росту погрешности. Но зато и к простоте и быстроте расчетов. Вот поэтому так важна линейность. Вот потому так к ней стремятся и так ее хотят.
Кстати, если еше раз посмотреть график линейной измерительной функции, то становится понятно, что она представляет собой не только математическую величину, но и чувствительность датчика прибора.

Чем круче подъем или спуск, тем быстрее изменяется выходная величина (электрический сигнал от датчика) в зависимости от значения физической величины, подаваемой на вход (температура, влажность, кислотность, напряженность электромагнитного поля и т.д.).

А это не всегда удобно. Например, если звук меняется слишком быстро, то шумомер будет просто не поспевать за его изменениями, и на экране будет быстро сменяющая друг друга чехарда цифр. Поэтому в большинстве шумомеров, предусматривается выбор метода измерения: fast (быстрый), slow (медленный). "Медленный" означает, что данные берутся за более длительный интервал, то есть усредняются.
Настраивается крутизна и для некоторых стационарных ph-метров.
"Мы обратили внимание вот на что : "А почему крутизна прямой настраивается только в стационарных, т.е. лабораторных приборах".
Справедливое замечание.
Хотя разница между бытовыми приборами и профессиональными часто размыта, все же к профессиональным можно отнести приборы, которые сертифицированы в Украине, то есть являются средством имерительной техники. Или по крайней мере имеет сертификат калибровки. В общем их заявленные характеристики подтверждены в метрологии. Это необходимо для ответственных измерительных задач, где нужно точно знать, что результата - "железный". Для бытовых приборов этого не требуется. А вот для профессиональных и вводится расширенный набор настроек - и подъем вверх-вниз путем корректировки по стандартным образцам прямой и даже изменение ее крутизны.

Завершение

Положа руку на сердце, мы все время говорим о том, что функция зависимости сигнала от датчика (физической величины) от электрического сигнала на выходе линейная. Точнее сказать - хотим этого. Но утверждать без проверочных тестов, что измерительная линия прямая, как полет стрелы, было бы верхом самонадеянности. Хотя если задаться целью, проверить это можно. Для этого нужно заполнить таблицу зависимости между входной физической величиной (поступающей на вход датчика - кислотность, температура, звук и т.д.) и выходным электрическим сигналом датчика, который потом поступает для обработки (усиления, преобразования) схемой прибора. По данным таблицы построить график и сразу станет понятно - прямая линия или нет. И там могут быть сюрпризы. На отдельных участках линия может изгибаться, превращаясь в кривую. А может и вовсе на всем диапазоне измерения мы заметим плавную "змею", а не прямую линию. Как в начале и конце графика крутизны нитратомера выше. А это уже говорит о росте погрешности. Или если пользоваться строгой терминологией - речь идет о метрологической неопределенности. То есть о невозможности точно предсказать, какое значение покажет прибор в той или иной точке прямой (кривой). Этой темой и пронизана наша вся сегодняшняя статья.
Если по результатам указанного теста прибора, выяснится, что ни о какой линейности и речи не идет, можна ожидать недовольные возгласы: "что-то ваш прибор показывает чепуху !". Подождите, а кто арбитр ? Чтобы делать такие обличающие выводы. Выясняется, что "чепуху" получили от криворуко собранного копеечного прибора. А вот на профессиональном приборе, который стоит в 10 раз дороже, это сделать поленились!
За достоверность измерения, простите за банальность и откровенность, придется заплатить. А также мы поверим в то, что у дорогих приборов, эта пресловутая линия, если не идеальная прямая, но максимально приближена к ней. Отсюда и минимальная метрологическая неопределенность. То есть обеспечена прогнозируемость и предсказуемость. И в этом ключевое преимущество измерительной прямой линии.