Що таке лінійність вимірювальних приладів і чому вона така важлива?
Дисплей вимірювального приладу як би він не був - сенсорний, рідкокристалічний або світлодіодний - не має значення, лише візуальне відображення електричних сигналів на виході мікросхеми - аналогово-цифрового перетворювача (мікроконтролера, мікропроцесора). По дорозі від датчика (старт) до дисплея (фініш) можуть бути фільтри, підсилювачі, перетворювачі. Але у будь-якому випадку всі маніпуляції після датчика проводяться вже з електрикою. Іншої "мови" прилади не розуміють. Більше того, прилад уявлення не має про те, що в природі існує є такий елемент, як датчик. Прилад працює лише з електричними сигналами. Йому абсолютно байдуже, чи датчик видає сигнал йому для обробки, чи ви втрутитесь в схему і підмініте датчик, замінивши таким чином один з електричних параметрів замість нього.

Кожен компонент вимірювального приладу має свою місію. І всі ці компоненти працюють як злагоджений оркестр. А хто ж диригент? Нехай це буде людина, яка тримає в руках прилад. Наш предок - це людина прямоходяча (Homo erectus). Йому на зміну прийшла людина розумна (Homo sapiens). А у нас виходить наступна реінкарнація - "людина, що вимірює" (Homo metiens - так це буде латиною). Тобто Homo metiens — це індивід, який не може жити без вологоміра, pH-метра і пірометра. Жарт. Хоча для майстрів у тій чи іншій галузі це на 100% відповідає дійсності. Без приладів вони, як без рук.
І їм важлива точність та достовірність. І сьогоднішня тема дозволить відкрити одну з дверей "кухні" вимірювальних приладів.
Введення в лінійну вимірювальну функцію
Головна місія у датчика – сприйняти фізичну величину (освітлення, вологість, кислотність) та перевести її в електричний імпульс.
Зазначимо ключовий момент для нашої сьогоднішньої розмови – є вхідна величина, а є вихідна. Це будівельний матеріал для функції. За однієї умови - має бути правило, закон, тобто ми повинні точно знати, за якого значення вхідної величини, яку ми отримаємо вихідну величину. В ідеалі так має бути. На практиці ж є набір факторів, що викривлюють результат, які прагнуть спотворити цю відповідність і внести елемент невизначеності (говорячи розумним словом "ентропія").
Блакитна мрія всіх виробників - щоб у всьому діапазон вимірювання приладу функція його датчика була лінійною.
Приклад із області ph метрів. Ось часткове завдання функції у табличному вигляді. Це ідеальний (лінійний) випадок. Та сама мрія. При зміні PH на 1 одиницю, напруга на виході PH електрода змінюється строго на 59,16 мВ.
| 1 PH | 177,48 мВ |
| 2 PH | 118,32 мВ |
| 3 PH | 59,16 мВ |
Практично всі pH-метри мають діапазон 0-14 pH. Так от, якщо на всьому цьому діапазоні ця лінійна залежність дотримувалася б, це була б і технічна реалізація (втілена в металі та пластиці) мрії інженерів – розробників того чи іншого бренду.
Чому? Причин кілька.
- Прогнозованість та передбачуваність. Ми можемо абсолютно точно знати в будь-якій точці графіка значення функції (мВ), якщо задамо значення PH. Це реально круто. Це все одно, що людині знати, що буде протягом кожного дня її довгого життя. Тільки чи захоче він це знати? Запитання. А ось для вимірювальних приладів (і розробників разом із ними) прогнозованість – це справжнє щастя. Якщо можна оперувати цим людським поняттям у цьому контексті.
- Простота та швидкість розрахунку. Лінійна функція вимагає дуже малих математичних потужностей для розрахунку. Навіть у думці можна порахувати значення. І цю здатність, на жаль, людство втрачає, покладаючись спочатку на калькулятори, а нині на смартфони. Оскільки маємо всього 2 елементарні математичні операції – множення та додавання. Ось формула для ph-метрів: E=E0−59,16×pH. Як бачимо, типова лінійна функція. E0 - початковий зсув верх-вниз графіка залежно від знака, а 59,16 - коефіцієнт, що визначає крутість функції (швидкість зростання чи падіння). У нас мінус, тому "падіння". Найбільш енергоємні та повільні операції, що навантажують процесор - це зведення в ступінь та вилучення кореня, диференціювання / інтегрування. Тому їх потрібно уникати.
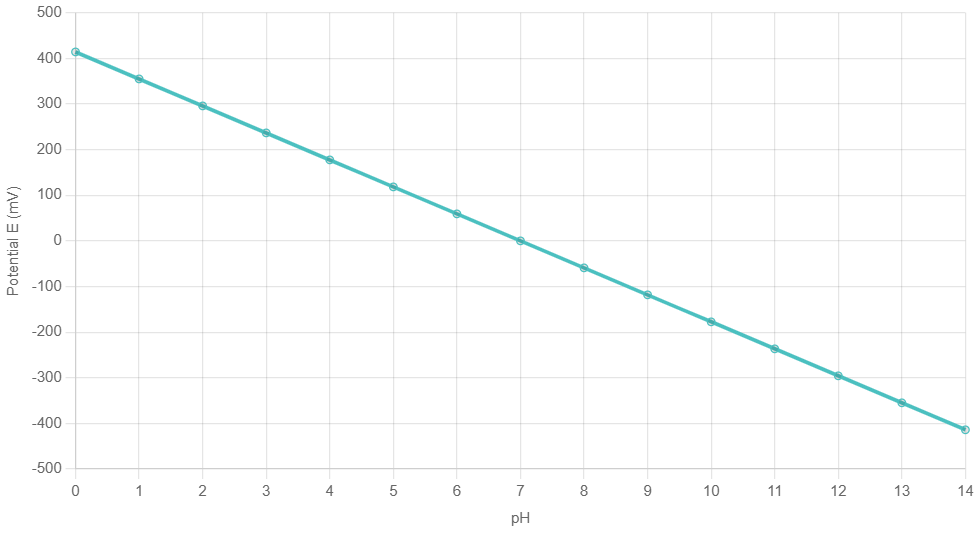
Так що пряма лінія, а відповідно лінійна, прогнозована та проста функція – це краса.
А от наприклад для квадратичної функції (не будемо наводити тут її графік, щоб не засмічувати пейзаж), тобто всім відома шкільна парабола, зі зростанням X все різкіше злітає вгору і Y (значення функції).
"А що, хіба парабола не передбачувана?" - Вигукне вдумливий і добре математично підкований читач. І буде правий. Адже квадратична функція теж описується однозначною формулою y=x2, за якою можна розрахувати значення y за будь-якого x. Тобто для функцій, навіть нелінійних, які на всій області визначення можна описати формулою (не приблизною з допустимим ступенем похибки, а точною), правило прогнозованості та передбачуваності безумовно виповнюється. Чого до речі не скажеш про простоту та швидкість розрахунку. Зведення в ступінь, особливо з великими показниками ступеня, є досить трудомісткою операцією для процесора.
Світ нелінійностей
Наведемо кілька прикладів.
Насправді ми живемо у світі нелінійностей. І часто з ними можна миритись. Ось кілька прикладів із різних сфер.
- Заряджання акумулятора (залежить від моделі - у Вас може бути по-іншому). Можна зауважити, що час на заряд 1% ємності в діапазоні 0-90% може бути в 1,5-2 рази менше (тобто заряджання йде швидше), ніж на той же 1% від 91 до 100%. Таке враження, що хтось заважає акумулятору і не дає йому заряджатися. Так, тут може впливати: температура батареї, особливості електрохімічних процесів на початку та в кінці циклу заряду (швидко чи повільно бере заряд). І зарядний пристрій може автоматично зменшувати струм ближче до кінця заряду. Але причина не важлива – графік заряду нелінійний.
- Залежність помилки пірометра від температури. Це особливо помітно за високотемпературними (широкодіапазонними інфрачервоними термометрами), як наприклад для IR-870 FLUS (одного з ТОПових промислових), представленим у нас на сайті. Наприклад при -10 ℃ помилка складе ±4℃, для 100 градусів ±2℃, для 1000 ±2℃. Це особливий різновид нелінійності - не безперервний, а ступінчастий. При переході через піддіапазон помилка змінюється стрибком (у бік зменшення чи збільшення). Наприклад у діапазонах від "до 0 ℃" до "от 0 до 500℃" помилка зменшується у 2 рази с ±4℃ до ±2℃.
Але передбачити та прогнозувати значення нелінійної фукнції, як для параболи (або гіперболи) або взагалі ступеневої та будь-якої іншої нелінійної функції, можна далеко не завжди. Особливо якщо немає формули для її опису.
Ось ми навели вище графік лінійної функції залежності різниці потенціалів на ph-електроді від значення PH. Він ідеальний, а життя вимірювальних приладів буває зовсім інакше.
Як добудовувати лінію ?
З курсу геометрії відомо, що для побудови лінії потрібно 2 точки. Одна – мало, три і більше підійдуть лише, якщо вони лежатимуть на одній прямій. Для ph-метрів, які мають функцію калібрування, можуть бути передбачені калібрування по 1, 2, 3 і більше точках.
Калібрування по 1-й точці якось не стикується з геометрією. Оскільки через одну точку можна провести безліч прямих. І кожна з цих прямих буде розташована під різним кутом до осі. А це, у свою чергу, означає, що ми не зможемо прогнозувати вихідне значення в залежності від вхідного, на всьому діапазоні, крім точки калібрування. Але то геометрія теоретично, а то практика приладів... А саме, розумна електронна начинка, яка "ухоплюється" лише за одну точку і цього виявляється достатньо для більш-менш точних вимірів у всьому діапазоні. Це як Шерлок Холмс міг за вкрай мізурними початковими даними, скласти повну картину злочину.
Пояснення може бути лише одне. Ми задаємо єдину точку на прямій, калібруючи прилад, наприклад, по буферному розчину ph=7.0. А як же прилад "дізнається", під яким кутом проходитиме крива пряма ? Тобто як добудувати пряму вліво та вправо на всьому діапазону виміру PH ?
Відповідь може бути тільки одна - в приладі "зашитий" алгоритм, який спираючись на результат калібрування, вибирає одну єдину пряму, і "домальовує" частини, яких бракує, ліворуч і праворуч.
У цьому величезна перевага і гнучкість цифрових вимірювальних приладів перед аналоговими. Наприклад стрілочними.
Між іншим і в стрілочних приладах часто-густо шкали можуть бути нелінійними. Тобто в одному піддіапазоні вимірювана величина зростає швидко, а в іншому - "ледве плететься". Це видно візуально - рисочки на шкалі то густо розташовані одна до одної, то між ними відстань відчутно збільшується. Це очевидна ознака нелінійності.
Ось це "добудова" або "домальовка" (ми свідомо спростили термін, щоб спростити розуміння) має дві усталеної назви, від яких так і віє науковістю: інтерполяція та екстраполяція. Пояснимо. Нехай ми відкалібрували ph-метр по двох точках: 4.01 і 7. Процес знаходження проміжних точок між цими двома точками називається ІНТЕРполяція ("інтер" - усередині), для чого існує набір математичних інструментів. А ось "добудова" за межами цього інтервалу (менше 4.01 і більше 7.0) називається ЕКСРАполяцією ("екстра" - поза).
Ми надто багато часу присвятили ph-метрам і частково пірометрам, але лінійність шкали бажана практично для всіх інших приладів. Особливо тепер після вищесказаного, відриваються очі у недосвідчених користувачів, які більше виконували рекомендації, наведені в інструкції, більше механічно, не вдаючись, що там стоїть у тому чи іншому приладі "під капотом".
Для людини прилад – це кнопки та дисплей. А прилад живе життям функцій, графіків залежностей та калібрування.
- наприклад, вологоміри зерна від торгової марки Supertech (Данія). У них можна ввести поправочний коефіцієнт і прилад перемістить - підніме вгору або вниз (залежить від знака поправки, що вводиться + або -) калібрувальну пряму, тим самим
наближаючись до істинизменшуючи помилку. Для введення поправочного коефіцієнта потрібен стандартний зразок зерна - еталон і, по суті, це аналог буферного розчину (із заздалегідь заданим PH). - у деяких шумомірах, навіть недорогих (а вже в шумомірах першого класу це як кажуть англомовні - must have) є можливість підстроювання - звичайною викруткою у найпростішому випадку за джерелом еталонного звуку заданої інтенсивності та частоти. Це джерело називається калібратор. І цей калібратор (вже за назвою зрозуміло, для чого він потрібен), по суті, дуже близький аналог камертону, за яким налаштовують музичні інструменти. У момент налаштування (калібрування) шумоміра, його вимірювальна функція (пряма залежність) також рухається трохи вгору або вниз.
- навіть такий оптичний інструмент, який і вимірювальним приладом язик не повертається назвати - аж надто він простий, як рефрактометр - у ньому немає ні електроніки (якщо не брати цифрові моделі), але навіть у ньому є гвинтик, який якщо підкрутити викруткою, теж рушить умовну пряму (графік функції) ближче до точного результату. А що є еталоном для рефрактометра? Калібрувальна рідина - дистильована вода або олія. До речі, для рефрактометрів ми трохи покривили душею, коли сказали, що калібруючи його, ми рухаємо умовну пряму. Не тільки умовну! Якраз при калібруванні, ми і побачимо, як смужка повинна стати рівно по центру. Ось десь віддалено нагадує щось подібне, тільки десь у надрах мікросхем, і відбувається при калібруванні приладів.
А крутість ?
Тобто, якщо прилад передбачає калібрування за еталоним зразком, ця пряма трохи переміщається вгору або вниз, щоб зменшити похибку.
"Вибачте !" Вдруге вигукне уважний і прискіпливий читач. "А чому ви говорите тільки про те, що пряма на Вашому графіку переміщується вгору чи вниз ?" Адже у наведеній вами формулі прямої є множник (наприклад у формулі для ph-метрів це 59,16), який визначає крутість, тобто швидкість зростання або зниження лінійної функції. А цю крутість не можна ніяк підлаштувати? Може згодом через старіння приладу не лише пряма "їде" вгору чи вниз, але й змінюється її кут нахилу?
Абсолютно справедливе зауваження. Щоб не крутити заїжджену платівку з приладами, про які ми вже тут говорили неодноразово, звернемося до лабораторних нітратомірів. Для них дійсно і окремо налаштовується такий показник, як крутість характеристики: залежність напруги від концентрації іонів. І тут не завжди вдається досягти лінійності! Особливо на початку та в кінці діапазону, де не рідко, виляючи хвостом, "пряма" згинається.
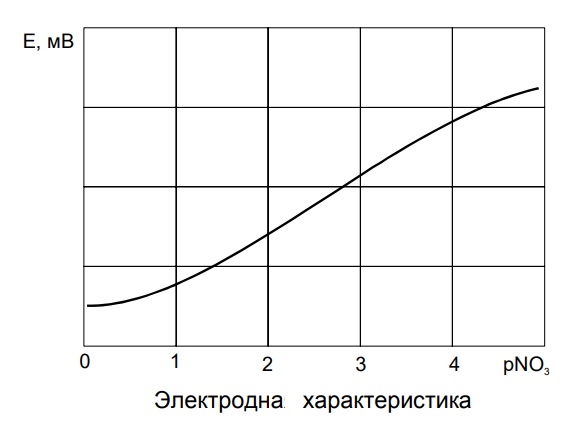
А отже, ніяка вона вже не пряма. А нелінійна функція. "Так що виходить, що для кожної ділянки буде своя формула ?" Так! І тепер Ви розумієте, наскільки складніше і описувати набором формул нелінійну функцію та рахувати її значення. До речі, далеко не завжди теоретично нелінійність можна описати формулою. Найчастіше якраз не можна. Намалюйте на аркуші паперу довільну криву лінію олівцем і спробуйте описати цю "функцію" формулою. Немає такої формули! Тому що це хаос. Тому доводиться викручуватися. Наприклад, замінюючи криволінійну ділянку прямолінійною. Звичайно, це призводить до зростання похибки. Зате і до простоти і швидкості розрахунків. Ось тому така важлива лінійність. Ось тому так до неї прагнуть і так її хочуть.
До речі, якщо ще раз подивитися графік лінійної вимірювальної функції, то стає зрозуміло, що вона є не тільки математичною величиною, а й чутливістю датчика приладу.
Чим крутіше підйом або спуск, тим швидше змінюється вихідна величина (електричний сигнал від датчика) залежно від значення фізичної величини, що подається на вхід (радіація, концентрація кисню у повітрі, лужність, напруженість електромагнітного поля тощо).
А це не завжди зручно. Наприклад, якщо звук змінюється занадто швидко, то шумомір просто не встигатиме за його змінами, і на екрані буде чехарда цифр, що швидко змінює одна одну. Тому в більшості шумомірів передбачається вибір методу вимірювання: fast (швидкий), slow (повільний). "Повільний" означає, що дані беруться за триваліший інтервал, тобто усереднюються.
Налаштовується крутість і для деяких стаціонарних ph-метрів.
"Ми звернули увагу ось на що: "А чому крутість прямої налаштовується тільки в стаціонарних, тобто в лабораторних приладах?"
Справедливе зауваження.
Хоча різниця між побутовими приладами та професійними часто розмита, все ж таки до професійних можна віднести прилади, які сертифіковані в Україні, тобто є засобом вимірювальної техніки. Або, принаймні, має сертифікат калібрування. Загалом, їх заявлені характеристики підтверджені в метрології. Це необхідно для відповідальних вимірювальних завдань, де потрібно точно знати, що результат - "залізний". Для побутових приладів це не потрібно. А ось для професійних і вводиться розширений набір налаштувань - і підйом вгору-вниз шляхом коригування за стандартними зразками прямої і навіть зміни її крутості.
Завершення
Поклавши руку на серце, ми весь час говоримо, що функція залежності сигналу від датчика (фізичної величини) від електричного сигналу на виході лінійна. Точніше сказати – хочемо цього. Але без перевірочних тестів стверджувати, що вимірювальна лінія пряма, як політ стріли, було б верхом самовпевненості. Хоча якщо поставити собі за мету, перевірити це можна. Для цього потрібно заповнити таблицю залежності між вхідною фізичною величиною (що надходить на вхід датчика - кислотність, температура, звук і т.д.) та вихідним електричним сигналом датчика, який потім надходить для обробки (посилення, перетворення) схемою приладу. За даними таблиці побудувати графік і одразу стане зрозуміло – пряма лінія чи ні. І там можуть бути сюрпризи. На окремих ділянках лінія може згинатися, перетворюючись на криву. А може взагалі на всьому діапазоні вимірювання ми помітимо плавну "змію", а не пряму лінію. Як на початку і наприкінці графіка крутості нітратоміра вище. А це вже говорить про зростання похибки. Або якщо користуватися суворою термінологією – йдеться про метрологічну невизначеність. Тобто про неможливість точно передбачити, яке значення покаже прилад у тій чи іншій точці прямої (кривої). Цією темою пронизана наша вся сьогоднішня стаття.
Якщо за результатами вказаного тесту приладу, з'ясується, що до лінійності далеко, можна очікувати незадоволені вигуки: "щось ваш прилад показує нісенітницю !". Зачекайте, а хто арбітр? Щоб робити такі безапеляційні висновки. З'ясовується, що "нісенітницю" отримали від найдешевшого приладу з аліекспресс. А ось на професійному приладі, який коштує в 10 разів дорожче, це зробити полінувались!
За достовірність виміру, вибачте за банальність та відвертість, доведеться заплатити. І тоді ми повіримо в те, що дорогі прилади мають цю лінію, якщо не ідеальну пряму, але максимально наближену до неї. Звідси й мінімальна метрологічна невизначеність. Тобто забезпечена прогнозованість та передбачуваність. І в цьому ключова перевага вимірювальної прямої лінії.